Graph Data Structure Interview Questions

Introduction

Graph-related interview questions are very common, and many algorithms you'll be expected to know fall into this category.

It's important to be acquainted with all of these algorithms - the motivation behind them, their implementations and applications.

If you're interested in reading more about Programming Interview Questions in general, we've compiled a lengthy list of these questions, including their explanations, implementations, visual representations and applications.

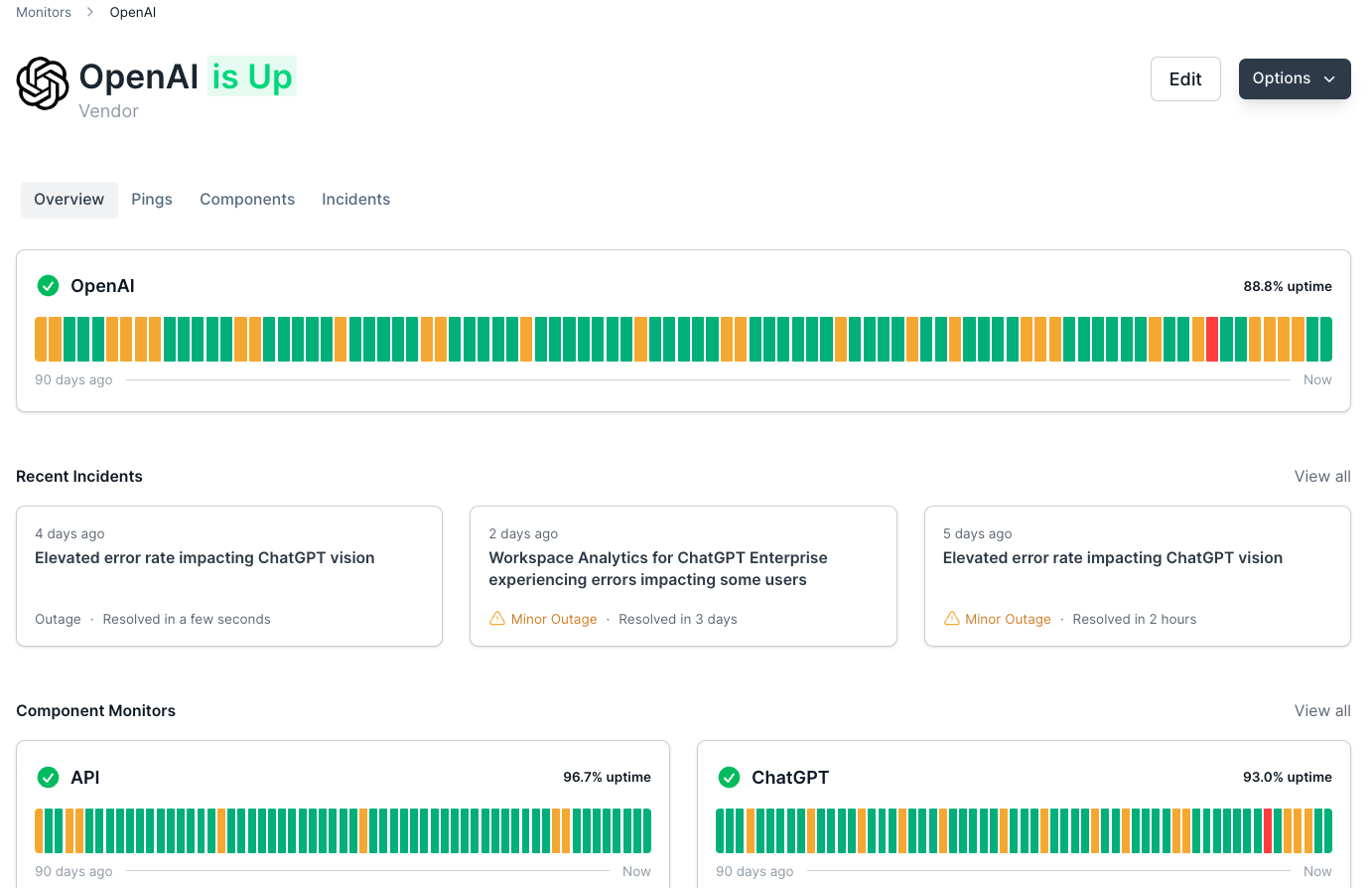
Graph Data Structure Interview Questions

Plainly said - a Graph is a non-linear data structure made up of nodes/vertices and edges.

Nodes are entities in our graph, and the edges are the lines connecting them:

Representation of a graph

There are many kinds of graphs, undirected graphs, directed graphs, vertex labeled graphs, cyclic graphs, edge-labeled graphs, weighted graphs etc.

Nonetheless, they are most often used to represent networks be it a city network, city streets, a terrain for AI to pass or social network connections.

Breadth First Search

Interview Question Example

Find the shortest path in a Maze. The path blocks are represented as 1 and the wall blocks are represented as 0. You can move in four directions (up, down, left, right).

                 0, 0, 0, 0, 0, 0, 0, 1, 1
                 0, 1, 1, 1, 1, 0, 0, 1, 0
                 0, 1, 0, 0, 1, 1, 1, 1, 0
                 1, 1, 1, 0, 1, 0, 0, 0, 0
                 1, 0, 1, 1, 1, 1, 1, 1, 1
                 1, 1, 0, 0, 0, 0, 0, 0, 0
                 0, 1, 0, 0, 1, 1, 1, 1, 0
                 0, 1, 0, 0, 1, 0, 0, 1, 0
                 0, 1, 1, 1, 1, 0, 0, 1, 1

Explanation

Breadth First Search (BFS for short) is a graph-traversal algorithm, often used for finding the shortest path from the starting node to the goal node.

BFS visits "layer-by-layer". This means that in a Graph like shown below, it first visits all the children of the starting node. These children are treated as the "second layer".

After visiting all the children of the starting node, the algorithm then visits all the children of the already visited children, practically moving to the third layer.

It's important to note that BFS will reach the end of the graph and then calculate the shortest path possible. It guarantees to find the shortest possible path, though it pays the price of not being as memory friendly as some other algorithms.

To accomplish this, BFS uses a Queue and this is an important feature of the algorithm. The terminal condition of the algorithm is that the Queue is empty, so it's going to go until it visits every single node.

Let's take a look at the pseudo-code behind the implementation:

Queue queue
node set visited true
queue.enqueue(node)

while queue not empty
    current = queue.dequeue()
    for v in current children
        if v is not visited
            v set visited true
            queue.enqueue(v)

We start off by adding the starting node to the queue. Since the queue is not empty, we set the current node to be the root node, and remove it from the queue.

We then check all of the current node's children and visit them if we haven't visited them before. After that, we add the children to the queue.

Each of these children will become the next current node. And since the queue data structure follows the FIFO (First in, first out) structure, we visit the rest of the children from the second layer, before continuing to visit the children from the proceeding layers.

BFS Applications

"Where can we use BFS?"

This algorithm is used in a lot of systems all around you! It's very often used for pathfinding, alongside Depth First Search. It's being used in your GPS Navigation system to find neighboring locations and even on social networking websites and search engines.

BFS found itself used a lot in artificial intelligence and machine learning, especially in robotics. And probably most noticeably, in your programming career, it's being used for garbage collection.

Depth First Search

Interview Question Example

Check if the given graph is strongly connected or not:

Explanation

Depth First Search (DFS) is another graph traversal algorithm, similar to Breadth First Search.

DFS searches as far as possible along a branch and then backtracks to search as far as possible in the next branch. This means that in the proceeding Graph, it starts off with the first neighbor, and continues down the line as far as possible.

Once it reaches the final node in that branch (1), it backtracks to the first node where it was faced with a possibility to change course (5) and visits that whole branch, in our case only (2).

Then it backtracks again to the node (5) and since it's already visited nodes (1) and (2), it backtracks to (3) and re-routes to the next branch (8).

The algorithm continues traversing in this fashion until all nodes have been visited and the stack is empty.

DFS doesn't guarantee to find the shortest possible path and can settle for a local optimum, unlike BFS. Thanks to this, it's more memory friendly, though not by a lot.

To accomplish this, DFS uses a Stack, which is the main difference between these two algorithms. A Stack follows a LIFO (Last-in, first-out) structure, which is the reason it goes as far as possible, before taking the other layers into consideration.

You can implement DFS with the help of recursion or iteration. The recursive approach is shorter and simpler, though both approaches are pretty much the same performance-wise.

Let's take a look at the recursive pseudo-code behind the implementation:

dfs(node)
node set visited true

for n in node neighbors
    if n is not visited
    dfs(n)

We start off by calling the algorithm on the given node and set that it's visited.

We then check all of the node's neighbors, and for each one, run the same algorithm if it isn't visited. This means that before advancing to the next neighbor, it visits all of the children of the first neighbor. Then goes back to the top, and visits the second neighbor - which advances the search for all of its children, and so on.

You might've noticed the lack of Stack in this example and I'd like to address it properly. Both approaches use a Stack structure in the background, though in the recursive approach, we don't explicitly define it like so.

Let's take a look at the iterative pseudo-code behind the implementation:

dfs(node)
    Stack stack
    node set visited true
    stack.push(node)

    while stack is not empty
        current = stack.pop()
        for n in node neighbors
            if n is not visited
                n set visited true
                stack.push(n)

Here, we add the starting node to the Stack. Since the stack is not empty, we set the current node to be the starting node and take it out of the stack.

We consider all of the neighbors, one by one. The first neighbor gets added to the stack, which makes it the new current node in the next iteration. This way, all of the children of this node will be checked before the node next to this one, from the original neighbor list.

DFS Applications

"Where can we use DFS?"

Similar to BFS, DFS is often used in artificial intelligence and machine learning. These two algorithms are very common and often compared.

DFS is generally used for pathfinding between nodes, and especially for finding paths for mazes! DFS is also used for topological sorting and finding strongly connected components.

A* Search

Given the following graph, where the black node is the starting node, the red nodes are the walls and the green node is the goal node, find the shortest path to the green node:

Explanation

A* Search is quite different than the two we've previously talked about. It's also a graph traversal algorithm, however, it's used to handle real-life pathfinding scenarios.

A* search relies on a knowledge and heuristic cost function for the given node as a way to decide which node it should visit next. In most cases, this cost function is denoted as f(x).

The cost function is calculated as a sum of two other functions:

• g(x) - The function that represents the cost of moving from the starting node to a given node.
• h(x) - The estimated cost from the given node to the goal node.

We obviously don't know the exact movement cost from the given note to the goal node, which is the reason why h(x) is also often referred to as the "heuristic".

The algorithm always picks the node with the lowest f(x) value. This is logical, considering how the function is calculated.

The fewer steps we take from the starting point combined with how close we get to the goal makes the value of f(x) lower if we're going with the shortest path to the goal. Walking away from the goal, and making more steps than needed to get there increases the f(x) function.

A* Search Applications

"Where can we use A* Search?

This algorithm is generally used for most of the shortest path problems. It's often used for real-life searching scenarios as well as video games. Most NPCs and AI players rely on A* to intelligently search for a path, fast and efficient.

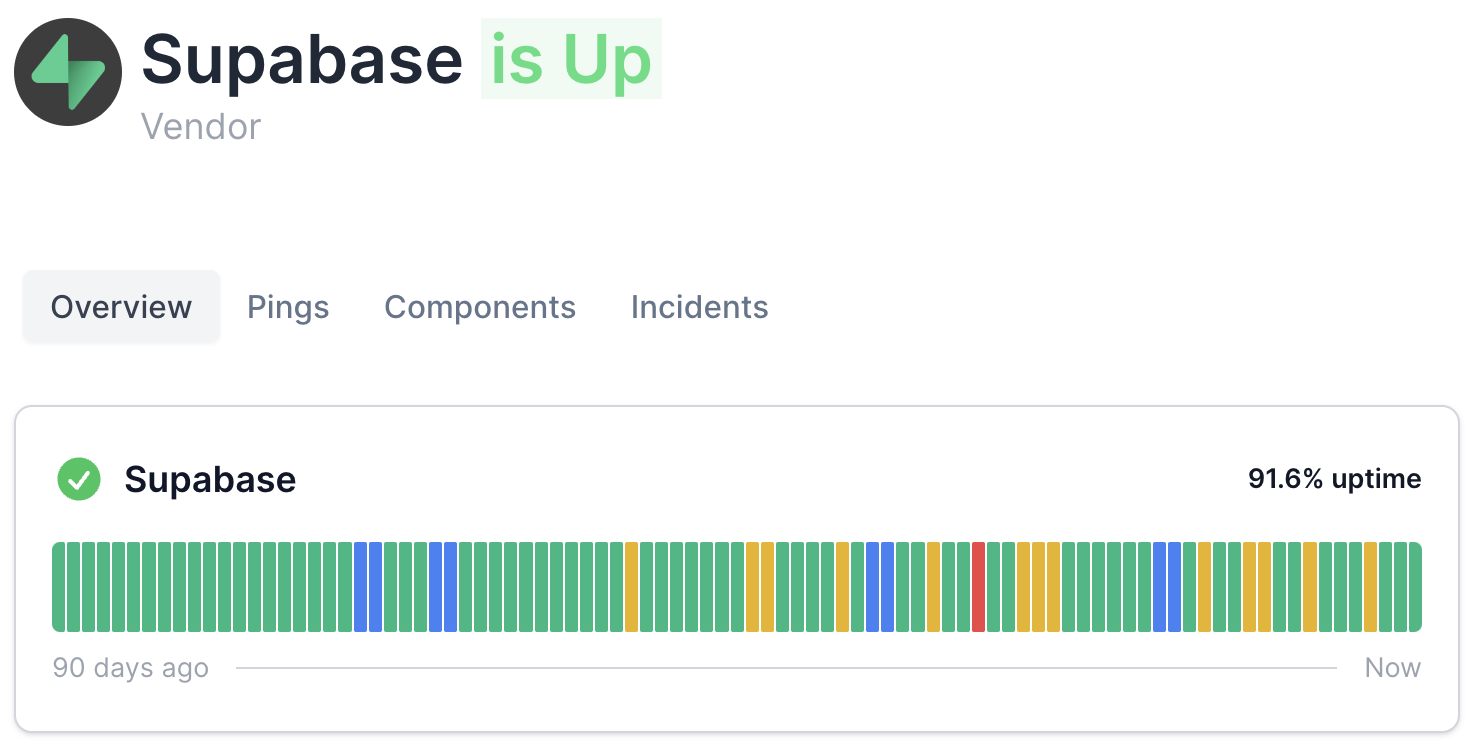
Dijkstra Algorithm

Given the following weighted graph, find the shortest path between the vertices A and H.

Explanation

Dijkstra Algorithm is a notorious graph traversal algorithm for finding the shortest path from a given node/vertex to another.

There are several implementations of this algorithm and some even use different data structures and have different applications. We'll cover the classic one - finding the shortest path between two nodes.

Dijkstra works in a slightly different fashion to the previous algorithms. Instead of starting at the root node, it starts at the goal node and backtracks its way to the starting node.

The algorithm does this by building a set of notes with the minimum distance from the source, dictated by the "weight" of the edges.

It's built with a few variables:

• dist - The distance from the goal node (most often referred to as the source node) to every other node in the graph. The dist to the source node is 0 since that's where we start. Additionally, the distance to all other nodes is set to infinity. As the algorithm traverses the graph, the distance to all other nodes gets recalculated according to the current node.
• Q - Similar to BFS, we need to define a Queue data type and fill it with all of the nodes from the graph. The terminal condition for the algorithm is if the Queue is empty.
• Set - We'll also need a set to contain all of the visited nodes, in order to not visit them again. In the end, the set will contain all nodes from the graph.

Let's take a look at the pseudo-code behind its implementation:

dijkstra(Graph, source)
    source set distance 0

    for n in Graph
        if n is not source
            n set dist infinity
            n set parent none
            queue.add(n)

    while Q is not empty
        n = node in Q with min dist(n)
        remove n from Q

        for node in n neighbors
            i = dist(n) + length(node, goal)
            if i < dist(goal)
                dist(goal) = i

Dijkstra Applications

"Where can we use Dijkstra?"

This algorithm is generally used for many of the shortest path problems, and it's most definitely a notable algorithm.

Google Maps uses Dijkstra to find the shortest path in navigation. IP Routing also relies heavily exactly on Dijkstra and it has applications in computer networking.

Comparing BFS, DFS, A* and Dijkstra

This might not pop out as an interview question, but it's most certainly a logical one. We've covered 4 different algorithms that are used mostly for the same purpose.

"Which one should I use? Which one is the best?"

The answer to this common question is: all of them.

Each of these algorithms, although seemingly similar, offer advantages over the other, based on the situation you're implementing them in and your specific case.

Here are some cases where you could be able to choose which one you would use:

• Finding currently alive members in a family tree.

In such a case, it would be best to use DFS since mostly the furthest levels are alive. BFS would waste too much time considering levels that shouldn't be considered. It wouldn't make sense to use Dijkstra or A* for this purpose.

• Finding the deceased members in a family tree.

In such a case, using DFS would be less practical than BFS as most of the deceased members would be located near the top. BFS would traverse this graph layer by layer and add all relevant members to the list.

• Finding the shortest path from point A to point B in a graph/map.

In such a case, although a bit controversial, using A* search over Dijkstra is common practice. Using BFS and DFS here can be very impractical. BFS assumes that the weight between all nodes is the same, whereas the actual weight/cost could vary. This is where Dijkstra comes into play!

Dijkstra takes the cost of moving on an edge into account. If the cost of going straight is bigger than going around it, it will go around. This may translate to congested roads on a map for an example.

A* focuses on reaching the goal, and only makes steps that seem promising and reasonable, according to its functions.

Dijkstra takes all other nodes into consideration, whereas A* only takes the reasonable ones. Because of this, A* is faster than Dijkstra and is often considered "the intelligent searching algorithm".

Some also refer to A* as the "informed" Dijkstra algorithm. If you take away the heuristic of A* - which means that it chooses the next step only according to the cost so far, you practically get Dijkstra, in reverse though. This makes A* run not greedily towards the goal, but rather in all directions considering every single node in the graph, which again is the same as Dijkstra.

If you're looking for an optimized search and results looking exclusively at the goal - A* is the choice for you.

If you're looking for an algorithm to compute the shortest path between the starting point and every single node in the tree, which includes the goal node - Dijkstra is the choice for you.

Resources

If you're looking for a better way to practice these kinds of programming interview questions, as well as others, then we'd recommend trying out a service like Daily Coding Problem. They'll send you a new problem to solve every day, all of which come from top companies. You can also find out more here if you want more info.

Conclusion

In this article, we've covered the common interview questions related to the graph data structure.

Again, if you're interested in reading more about Programming Interview Questions in general, we've compiled a lengthy list of these questions, including their explanations, implementations, visual representations and applications.