Bubble Sort in Python

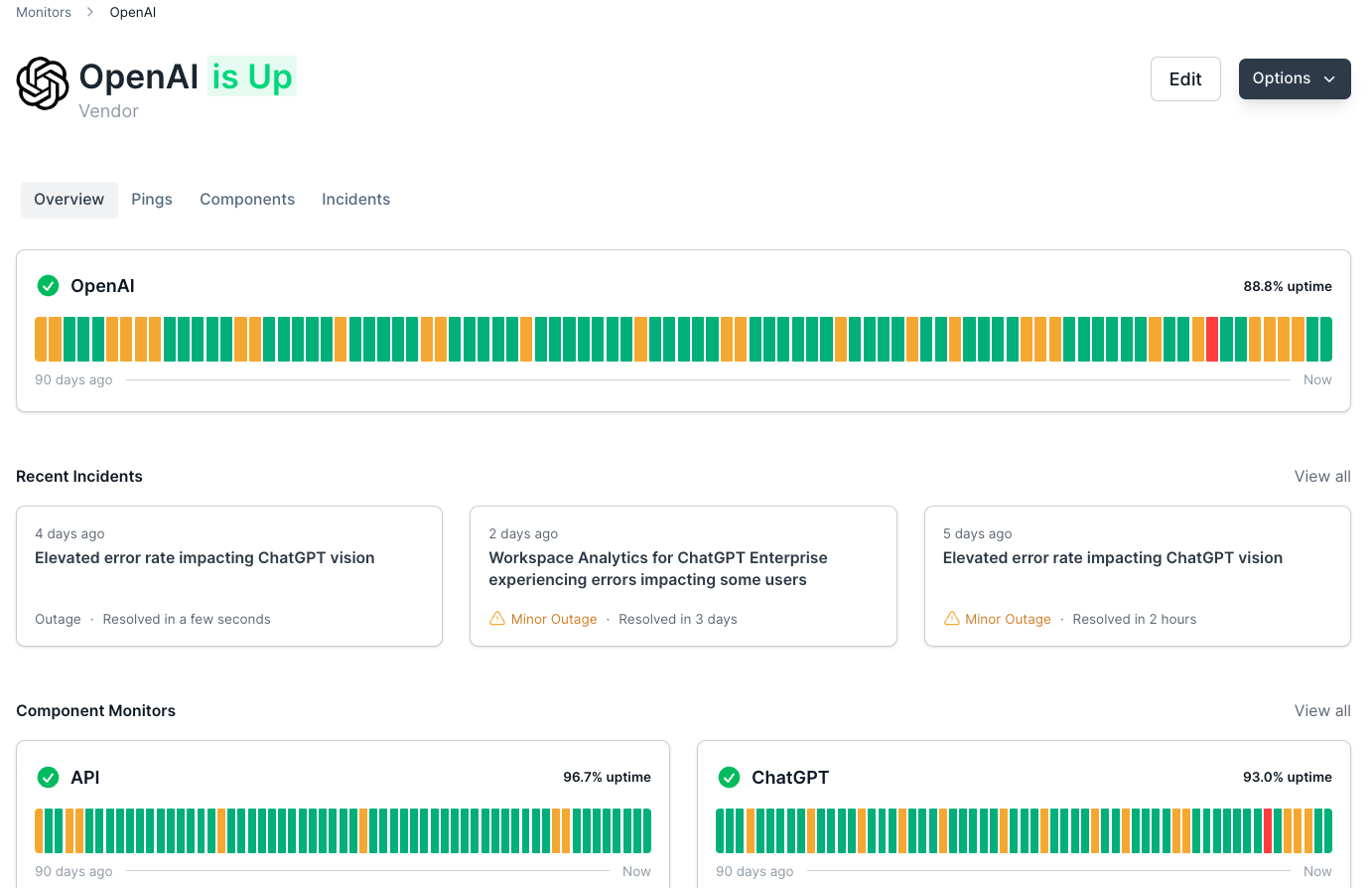
Introduction

For most people, Bubble Sort is likely the first sorting algorithm they heard of in their Computer Science course.

It's highly intuitive and easy to "translate" into code, which is important for new software developers so they can ease themselves into turning ideas into a form that can be executed on a computer. However, Bubble Sort is one of the worst-performing sorting algorithms in every case except checking whether the array is already sorted, where it often outperforms more efficient sorting algorithms like Quick Sort.

The Idea Behind the Bubble Sort

The idea behind Bubble Sort is very simple, we look at pairs of adjacent elements in an array, one pair at a time, and swap their positions if the first element is larger than the second, or simply move on if it isn't. Let's look at an example and sort the array [8, 5, 3, 1, 4, 7, 9]:

If you focus on the first number, the number 8, you can see it "bubbling up" the array into the correct place. Then, this process is repeated for the number 5 and so on.

How to Implement Bubble Sort in Python

With the visualization out of the way, let's go ahead and implement the algorithm. Again, it's extremely simple:

def bubble_sort(our_list):
    # We go through the list as many times as there are elements
    for i in range(len(our_list)):
        # We want the last pair of adjacent elements to be (n-2, n-1)
        for j in range(len(our_list) - 1):
            if our_list[j] > our_list[j+1]:
                # Swap
                our_list[j], our_list[j+1] = our_list[j+1], our_list[j]

Now, let's populate a list and call the algorithm on it:

our_list = [19, 13, 6, 2, 18, 8]
bubble_sort(our_list)
print(our_list)

This will give us:

[2, 6, 8, 13, 18, 19]

Optimization

The simple implementation did its job, but there are two optimizations we can make here.

When no swaps are made, that means that the list is sorted. However, with the previously implemented algorithm, it'll keep evaluating the rest of the list even though it really doesn't need to. To fix this, we'll keep a boolean flag and check if any swaps were made in the previous iteration.

If no swaps are made, the algorithm should stop:

def bubble_sort(our_list):
    # We want to stop passing through the list
    # as soon as we pass through without swapping any elements
    has_swapped = True

    while(has_swapped):
        has_swapped = False
        for i in range(len(our_list) - 1):
            if our_list[i] > our_list[i+1]:
                # Swap
                our_list[i], our_list[i+1] = our_list[i+1], our_list[i]
                has_swapped = True

The other optimization we can make leverages the fact that Bubble Sort works in such a way that the largest elements in a particular iteration end up at the end of the array.

The first time we pass through the list the position n is guaranteed to be the largest element, the second time we pass through the position n-1 is guaranteed to be the second-largest element, and so forth.

This means that with each consecutive iteration we can look at one less element than before. More precisely, in the k-th iteration, only need to look at the first n - k + 1 elements:

def bubble_sort(our_list):
    has_swapped = True

    num_of_iterations = 0

    while(has_swapped):
        has_swapped = False
        for i in range(len(our_list) - num_of_iterations - 1):
            if our_list[i] > our_list[i+1]:
                # Swap
                our_list[i], our_list[i+1] = our_list[i+1], our_list[i]
                has_swapped = True
        num_of_iterations += 1

Optimized vs Non-Optimized Bubble Sort

Let's go ahead and compare the time it takes for each of these code snippets to sort the same list a thousand times using the timeit module:

Unoptimized Bubble Sort took: 0.0106407

Bubble Sort with a boolean flag took: 0.0078251

Bubble Sort with a boolean flag and shortened list took: 0.0075207

There isn't much of a difference between the latter two approaches due to the fact that the list is extremely short, but on larger lists - the second optimization can make a huge difference.

Conclusion

In the most inefficient approach, Bubble Sort goes through n-1 iterations, looking at n-1 pairs of adjacent elements. This gives it the time complexity of \)O(n^2)\), in both best-case and average-case situations. \)O(n^2)\) is considered pretty horrible for a sorting algorithm.

It does have an O(1) space complexity, but that isn't enough to compensate for its shortcomings in other fields.

However, it's still a big part of the software development community and history, and textbooks almost never fail to mention it when talking about basic sorting algorithms.