Linear Search in Python

Linear Search, also known as Sequential Search, operates by traversing through the dataset, element by element until the desired item is found or the algorithm reaches the end of the collection. Its simplicity and ease of implementation make it a go-to choice for small datasets and lists where items are added or removed frequently.

While it may not boast the efficiency of its more complex counterparts like Binary Search, Linear Search can be pretty useful in various practical use cases, especially when dealing with unsorted data.

In this article, we'll delve deeper into the inner workings of Linear Search, illustrating its mechanism with practical Python examples, and dissecting its performance through complexity analysis.

How Does Linear Search Work?

Linear Search, as the name suggests, operates in a straightforward, linear manner, systematically examining each element in the dataset until the desired item is located or the end of the dataset is reached. It doesn’t require the data to be in any particular order and works equally well with both sorted and unsorted datasets.

Let’s break down its operation into a step-by-step process:

1. Start at the Beginning

   • Linear Search starts at the first element of the dataset. It compares the target value (the value we are searching for) with the first element.

2. Compare and Move

   • If the target value matches the current element, congratulations! The search is successful, and the index (or position) of the current element is returned. If a match is not found, the algorithm moves to the next element in the sequence.

3. Repeat

   • This process of moving from one element to the next and comparing each with the target value continues sequentially through the dataset.

4. Conclusion of Search

   • Item Found: If the algorithm finds an element that matches the target value, it returns the index of that element.

   • Item Not Found: If the algorithm reaches the end of the dataset without finding the target value, it concludes that the item is not present in the dataset and typically returns a value indicating an unsuccessful search (such as -1 or None in Python).

Linear Search is particularly useful due to its simplicity and the fact that it can be used on both sorted and unsorted datasets.

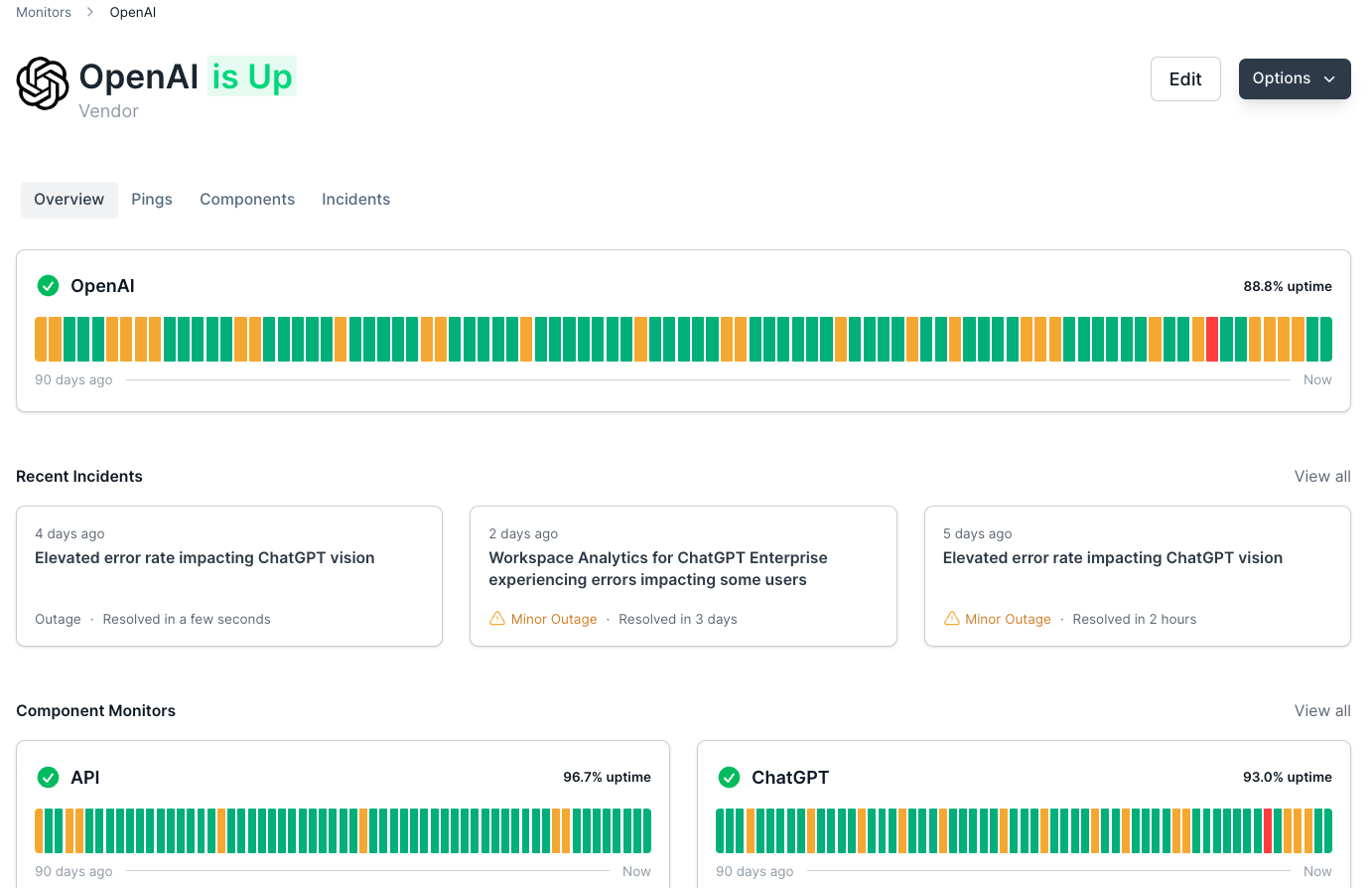
Linear Search - Example

Now that we understand how Linear Search works in theory, let’s delve into a tangible example to visualize its operation. Say we are searching the following list of numbers:

numbers = [21, 39, 46, 52, 63, 75]

And let’s say we want to find the number 52:

• Step 1: Start with the first number - 21
  • Compare it with 52 - they are not equal
• Step 2: Move to the next number -39
  • Compare it with 52 - still not equal
• Step 3: Move to the next number - 46
  • Compare it with 52 - not equal
• Step 4: Move to the next number - 52
  • Finally, they are equal!
  • Return the index 3 as the successful search result.

The following illustration visually represents the process we've just described:

In the upcoming sections, we will dive into the Pythonic world to implement Linear Search and explore its complexity in terms of time and space to understand its efficiency and limitations.

How to Implement Linear Search in Python

After exploring the conceptual framework and walking through an example of Linear Search, let’s dive into Python to implement this algorithm.

First of all, we'll define a function that will wrap the logic of the linear search - let's call it linear_search(). It should take two parameters - arr (the list to search through) and target (the item to search for):

def linear_search(arr, target):

Now, this function will perform a linear search on a list arr for a target value. It should return the index of target in arr if found, and -1 otherwise.

We can finally get to the core of the linear search algorithm - looping through the list and comparing the current element with the target. We'll do so by iterating through each element item and its corresponding index in the list arr using the enumerate function:

def linear_search(arr, target):
    for index, item in enumerate(arr):
        if item == target:
            return index  # Target found, return the index
    return -1  # Target not found, return -1

Let’s utilize our linear_search() function to find an item in a list:

books = ["The Great Gatsby", "Moby Dick", "1984", "To Kill a Mockingbird", "The Hobbit"]
target_book = "1984"

# Using the linear_search function
index = linear_search(books, target_book)

# Output the result
if index != -1:
    print(f"'{target_book}' found at index {index}.")
else:
    print(f"'{target_book}' not found in the list.")

This will result in:

'1984' found at index 2.

In the upcoming sections, we will delve into the complexity analysis of Linear Search, exploring its efficiency and discussing scenarios where it shines and where other algorithms might be more suitable.

Complexity Analysis

Understanding the complexity of an algorithm is crucial as it provides insights into its efficiency in terms of time and space, thereby allowing developers to make informed decisions when choosing algorithms for specific contexts. Let’s dissect the complexity of Linear Search:

Time Complexity

The best-case scenario occurs when the target element is found at the first position of the array. In this case, only one comparison is made, resulting in a time complexity of O(1). The worst-case scenario happens when the target element is at the last position of the array or is not present at all. Here, the algorithm makes n comparisons, where n is the size of the array, resulting in a time complexity of O(n). On average, the algorithm may have to search through half of the elements, resulting in a time complexity of O(n/2). However, in Big O notation, we drop the constant factor, leaving us with O(n).

Space Complexity

Linear Search is an in-place algorithm, meaning it doesn’t require additional space that grows with the input size. It uses a constant amount of extra space (for variables like index and item), and thus, the space complexity is O(1).

In the context of practical applications, Linear Search can be quite useful in scenarios where the simplicity of implementation is a priority, and the datasets involved are not prohibitively large. However, for applications where search operations are frequent or the datasets are large, considering algorithms with lower time complexities might be beneficial.

Linear Search vs. Binary Search

Linear Search, with its simplicity and ease of implementation, holds a unique position in the world of search algorithms. However, depending on the context, other search algorithms might be more efficient or suitable. Let’s delve into a comparative analysis between Linear Search and its main competitor in the space of search algorithms - Binary Search.

	Linear Search	Binary Search
Prerequisites	No prerequisites regarding the order of the dataset.	Requires the dataset to be sorted.
Time Complexity	O(n) in the worst and average cases.	O(logn) in the worst and average cases.
Use-Cases	Suitable for smaller and/or unordered datasets.	Ideal for larger, sorted datasets, especially where search operations are frequent.
Implementation	Simpler to implement.	Slightly more complex due to the need to manage the high and low pointers during the search.